Calculate Probability

Binomial probability calculations can be complex and time-consuming, especially when dealing with large datasets or multiple scenarios. For statisticians and researchers working with binary outcomes, whether analyzing clinical trial results, quality control data, or survey responses, having access to a reliable, efficient calculator is essential for accurate statistical analysis.

Our comprehensive binomial probability calculator offers advanced features that go beyond basic calculations, providing exact and cumulative probabilities while solving for the number of trials needed.

Understanding Binomial Probability

Binomial probability deals with experiments that have exactly two possible outcomes: success or failure, yes or no, defective or non-defective. These experiments, known as Bernoulli trials, form the backbone of many statistical analyses across industries.

Key Characteristics of Binomial Experiments

A binomial experiment must satisfy four critical conditions:

• Fixed number of trials: The experiment involves a predetermined number of independent trials (n)
• Binary outcomes: Each trial results in exactly two possible outcomes
• Constant probability: The probability of success (p) remains the same for each trial
• Independence: The outcome of one trial doesn’t affect any other trial

The Binomial Formula Explained

The binomial probability formula calculates the likelihood of achieving exactly x successes in n trials:

P(X = x) = C(n,x) × p^x × (1-p)^(n-x)

Where:

• n = number of trials
• x = number of successes
• p = probability of success on a single trial
• C(n,x) = binomial coefficient (“n choose x”)

Using Our Advanced Binomial Probability Calculator

Our calculator stands out from competitors by offering comprehensive functionality in an intuitive interface. Here’s your step-by-step guide to maximizing its capabilities:

Step 1: Input Your Parameters

Start by entering your basic parameters:

• Number of trials (n): Enter the total number of experiments or observations
• Probability of success (p): Input the probability as a decimal (0.5 for 50%) or fraction (1/2)
• Number of successes (x): Specify the exact number of successful outcomes you’re analyzing

Step 2: Choose Your Calculation Type

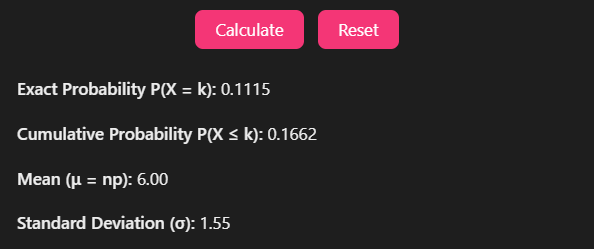
Our calculator offers multiple probability calculations:

• Exact probability: P(X = x) – probability of exactly x successes
• Cumulative probability: P(X ≤ x) – probability of x or fewer successes
• Complementary probability: P(X > x) – probability of more than x successes

Step 3: Advanced Solver Functions

Unlike many competitors, our calculator can solve for the number of trials needed. Simply:

• Input your desired probability threshold
• Specify the minimum number of successes required
• Let the calculator determine the optimal number of trials

Practical Examples and Real-World Applications

Example 1: Coin Toss Analysis

Problem: What’s the probability of getting exactly 5 heads in 10 coin tosses?

Solution using our calculator:

• Number of trials (n): 10
• Probability of success (p): 0.5
• Number of successes (x): 5

Result: P(X = 5) = 0.246 or 24.6%

This calculation shows that getting exactly 5 heads in 10 tosses occurs about 1 in 4 times.

Example 2: Lottery Draw Probabilities

Problem: A lottery has a 2% chance of winning per ticket. If you buy 50 tickets, what’s the probability of winning at least once?

Solution:

• Number of trials (n): 50
• Probability of success (p): 0.02
• Calculate P(X ≥ 1) = 1 – P(X = 0)

Result: P(X ≥ 1) = 0.636 or 63.6%

Example 3: Soccer Game Attendance

Problem: Historical data shows 85% attendance rate for soccer games. For a 22-player roster, what’s the probability that exactly 18 players attend?

Solution:

• Number of trials (n): 22
• Probability of success (p): 0.85
• Number of successes (x): 18

Result: P(X = 18) = 0.196 or 19.6%

Example 4: Manufacturing Quality Control

Problem: A production line has a 3% defect rate. In a batch of 100 items, what’s the probability of finding 2 or fewer defective items?

Solution:

• Number of trials (n): 100
• Probability of success (p): 0.03 (defining defect as “success” for calculation purposes)
• Calculate P(X ≤ 2)

Result: P(X ≤ 2) = 0.419 or 41.9%

Example 5: Marketing Conversion Analysis

Problem: An email campaign has a 12% conversion rate. With 500 recipients, what’s the probability of achieving 50-70 conversions?

Solution:

• Number of trials (n): 500
• Probability of success (p): 0.12
• Calculate P(50 ≤ X ≤ 70)

Result: P(50 ≤ X ≤ 70) = 0.847 or 84.7%

Advanced Features That Set Us Apart

Unique Trial Solver Capability

Our calculator’s standout feature is its ability to determine the number of trials needed to achieve a desired probability. This reverse-calculation capability is invaluable for:

• Experimental design: Planning how many subjects you need for reliable results
• Quality assurance: Determining optimal sample sizes for testing
• Risk assessment: Calculating required iterations to achieve confidence thresholds

Comprehensive Probability Outputs

While competitors often provide limited results, our calculator delivers:

• Exact binomial probabilities
• Cumulative distribution values
• Complementary probabilities
• Mean and standard deviation calculations
• Confidence intervals for probability estimates

Enhanced User Experience

Our interface addresses common usability issues found in competitor tools:

• Intuitive design: Clean, professional layout suitable for academic and professional use
• Multiple input formats: Accept decimals, percentages, or fractions
• Instant calculations: Real-time results as you adjust parameters
• Export functionality: Save results for reports and presentations

Benefits of Using Our Binomial Calculator in 2025

Accuracy and Reliability

Our calculator uses advanced algorithms to ensure precision across all calculation types. Whether you’re working with small samples or large datasets, the results maintain statistical accuracy essential for professional research.

Time Efficiency

Manual binomial calculations can take hours, especially for complex scenarios. Our calculator reduces calculation time from hours to seconds, allowing you to focus on analysis and interpretation rather than computation.

Accessibility and Convenience

Available 24/7 from any device with internet access, our calculator eliminates the need for specialized software or statistical packages for binomial probability calculations.

Educational Value

The step-by-step breakdown helps users understand the underlying mathematics, making it valuable for both learning and verification purposes.

Frequently Asked Questions

What’s the difference between exact and cumulative probability?

Exact probability calculates the likelihood of achieving exactly x successes, while cumulative probability calculates the likelihood of achieving x or fewer successes. For example, if you’re flipping 10 coins, exact probability tells you the chance of getting exactly 5 heads, while cumulative probability tells you the chance of getting 5 or fewer heads.

Can I use this calculator for experiments with more than two outcomes?

No, binomial probability specifically applies to experiments with exactly two outcomes. 

How do I know if my data follows a binomial distribution?

Your data follows a binomial distribution if it meets these criteria: fixed number of independent trials, each trial has exactly two possible outcomes, constant probability of success across trials, and independence between trials.

Calculate Probabilities with Ease

Our free binomial probability calculator represents the next generation of statistical tools, combining advanced functionality with user-friendly design. Whether you’re conducting research, analyzing quality control data, or exploring probability concepts, our calculator provides the accuracy and efficiency you need.

Ready to streamline your binomial probability calculations? Access our free calculator now and discover how advanced statistical computing can enhance your research and analysis capabilities.