Matrix Rank Calculator 2025
Result
Rank: -
-
Understanding matrix rank is essential for solving linear equations, analyzing data relationships, and tackling complex engineering problems. Whether you’re a student struggling with linear algebra homework or a data scientist working with large datasets, calculating matrix rank manually can be time-consuming and error-prone.
Our free matrix rank calculator 2025 eliminates these challenges by providing instant, accurate results with detailed step-by-step solutions.
What is the Matrix Rank?
Matrix rank measures the maximum number of linearly independent rows or columns in a matrix. Think of it as a way to determine how much “useful information” your matrix contains. A matrix with higher rank has more independent information, while lower rank indicates redundancy in the data.
The rank of a matrix equals the number of non-zero rows in its row echelon form. This concept helps us understand whether systems of linear equations have unique solutions, multiple solutions, or no solutions at all.
Importance of Understanding Matrix Rank
Matrix rank serves as a foundation for numerous mathematical and practical applications. Engineers use it to analyze structural stability, data scientists apply it for dimensionality reduction, and financial analysts rely on it for risk assessment models.
Understanding matrix rank helps you determine the solvability of linear systems, identify data dependencies, and optimize computational algorithms. This knowledge becomes particularly valuable when working with large datasets where manual calculations would be impossible.
Methods to Calculate Matrix Rank
Elementary Row Operations
Elementary row operations form the backbone of matrix rank calculation. These operations include:
- Swapping two rows
- Multiplying a row by a non-zero constant
- Adding a multiple of one row to another row
These operations preserve the rank while transforming the matrix into a more manageable form.
Row Echelon Form
Converting a matrix to row echelon form reveals its rank clearly. In row echelon form, each row has more leading zeros than the row above it, and all non-zero rows appear above zero rows.
The rank equals the number of non-zero rows in this form. This systematic approach ensures accurate results every time.
Step-by-Step Calculation Guide
Start by writing your matrix in standard form. Apply elementary row operations to create zeros below the leading coefficient of each row. Continue this process column by column, moving from left to right.
Once you achieve row echelon form, count the non-zero rows. This number represents your matrix rank. Remember that any row consisting entirely of zeros doesn’t contribute to the rank.
Using Our Free Matrix Rank Calculator in 2025
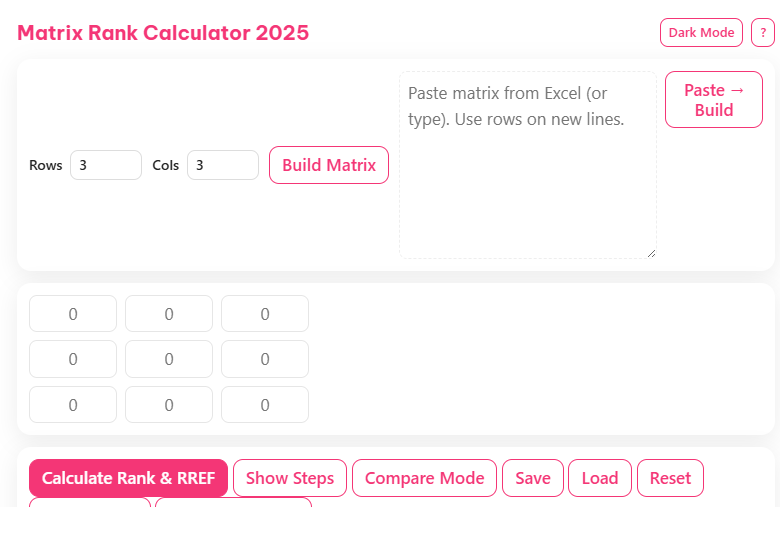
Our calculator simplifies the entire process with its intuitive interface and powerful computational engine. Simply input your matrix elements, and our tool instantly provides the rank along with the complete solution process.
The calculator handles matrices of various sizes and formats, accommodating integers, fractions, decimals, and even complex numbers. This versatility makes it suitable for academic, professional, and research applications.
Benefits of Using Our Calculator
Speed and Efficiency
Calculate matrix rank in seconds rather than spending hours on manual computations. Our optimized algorithms handle even large matrices with remarkable speed.
Error-Free Results
Eliminate calculation mistakes that commonly occur during manual row operations. Our calculator ensures 100% accuracy every time.
Educational Value
Learn from detailed step-by-step solutions that show each row operation clearly. This feature helps students understand the underlying process while providing quick answers.
Features to Look for in a 2025 Calculator
Modern matrix rank calculators should offer comprehensive functionality beyond basic calculations. Essential features include step-by-step solutions that break down each row operation, clear display of row echelon form, and ability to handle large matrices efficiently.
Advanced features like error detection, multi-platform support, and integration capabilities distinguish premium calculators from basic tools. Our 2025 calculator incorporates all these features plus innovative additions like complex number support, customizable precision, and cloud storage integration.
The user interface should remain simple despite advanced functionality. Look for calculators that offer intuitive design, clear visualizations of matrix transformations, and comprehensive educational resources.
Examples of Matrix Rank Calculations
Example 1: Calculating Rank by Hand
Consider matrix A:
A = | 1 2 |
| 3 4 |
To find the rank manually, we perform row operations. Subtract 3 times the first row from the second row:
| 1 2 |
| 0 -2 |
Since both rows are non-zero, the rank equals 2.
Example 2: Verifying with Our Free Calculator
Let’s verify using matrix B:
B = | 1 2 3 |
| 2 4 6 |
Using our calculator, we input these values and instantly see that the rank equals 1. The calculator shows that the second row is exactly twice the first row, making them linearly dependent.
The step-by-step solution reveals how row operations eliminate the dependency, resulting in:
| 1 2 3 |
| 0 0 0 |
Advanced Concepts and Applications
Linear Independence and Matrix Rank
Matrix rank directly relates to linear independence. The rank tells us the maximum number of linearly independent vectors we can select from the matrix rows or columns. This concept proves crucial in vector spaces and basis construction.
When vectors are linearly independent, no vector can be expressed as a combination of others. This independence is what gives the matrix its “information content” measured by rank.
Applications in Various Fields
Data scientists use matrix rank for principal component analysis, reducing dataset dimensions while preserving essential information. Engineers apply it in circuit analysis, structural mechanics, and control systems design.
Financial analysts rely on matrix rank for portfolio optimization and risk modeling. The rank helps identify redundant assets and optimize investment strategies. Machine learning algorithms use rank to prevent overfitting and improve model generalization.
Troubleshooting Common Issues
Users sometimes encounter difficulties with input formatting or interpreting results. Our calculator includes comprehensive error detection that identifies formatting issues and suggests corrections.
When working with very large matrices, computational limitations may affect performance. Our advanced algorithms optimize processing for maximum efficiency while maintaining accuracy.
Complex numbers and fractional inputs require special attention. Our calculator handles these automatically, but users should verify their input format matches our specified guidelines.
Get Started Today
Matrix rank calculation no longer needs to be a tedious, error-prone process. Our free matrix rank calculator 2025 combines cutting-edge technology with educational value, making it the perfect tool for students, professionals, and researchers.
Experience the difference that advanced algorithms, comprehensive features, and intuitive design can make in your mathematical workflow. Whether you’re solving homework problems, conducting research, or tackling complex engineering challenges, our calculator provides the accuracy and efficiency you need.
Calculate Matrix Rank Instantly with our free tool and discover how technology can transform your approach to linear algebra problems.